方法与程序

钢琴是十二平均律乐器。它所发出的音，除同度和八度完全协和外，其他各种音程都不同程度地偏离纯律那样的频率呈简单整数比的“纯”。

倘若以某一音为起点去直接一个一个地分别调准八度内的12个音，那将是难以做到的。一般来说，在小字组和小字一组，以纯正音程的“纯点”作为“参照点”，以拍频作为“尺度”，四度、五度、三度、六度还是可以调得合乎要求；至于二度、七度以及增四度、减五度就很难调准了，即便是有受过严格训练的“音乐的耳朵”，调出来的音也难以达到艺术上的要求。

经验证明，在钢琴上调好十二平均律，需要分几个程序来完成：

(1)首先靠听拍音建立(调准)一个基准音组(生成一个八度内的12个音)。基准音组通常设在小字组与小字一组之内(原因后述)。

(2)利用同度的“纯”(无拍音)调准各同音弦。

(3)利用八度的“纯”完成基准音组基础上的扩展调音，即调准基准音组上方及下方其他各组的音。

基准音组的分律方法与程序多种多样，并不强求一致，只要能把音程分准确，即不失为一种可行的方法。不同方法会有各自的优势与不足，对于不同的调律者的适应性也不一样。现举几例如下。

五度、八度分律法：

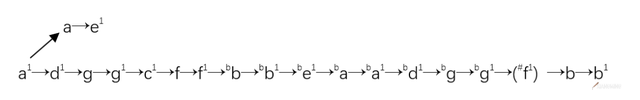
四度、五度循环法：

[上五下四]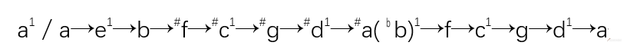

[上四下五]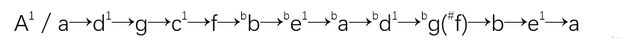

三度、五度循环法：

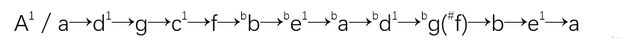
三度、六度循环法：

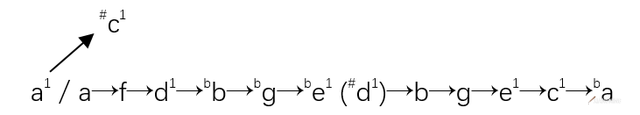
基准音组的建立方法与程序可以说五花八门，除上述者外，还有许多变通的方法。其间有不少相似的地方。

如：

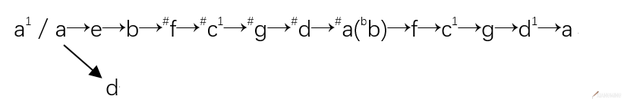
这种方法并未严格遵循上五下四的程序，而且音区偏低(d—d1)。

还有些方法基本属于上四下五或上五下四的循环方法，只是多了一些音，增加了一些转位音程及八度的检验。

近年来，国内有人提出“分叉二枝生律法”★[z1] ，目的是减少(生律过程中)依赖的环节数，即减少人为的误差(积累)。

这种生律法的特点是：由a音开始分两路生律，一路上四下五，至第6步骤生律为bel；另一路上五下四，至第6步生律为#d1。bel与#d1为同音异名，两音相合时说明基准音组大体合乎要求，如下图

综观以上基准音组生律法不难看出，所采用的音程不是四五度，就是大三、大六度。这是因为在小字组和小字一组的四五度和大三、大六度的拍速较慢或适中，较易分辨(参见后面的“拍频表”)。

在我国，上述的各种分律法，虽见于不同的文献资料，但实际应用上主要是四五度循环法，其中的上五下四循环法应用较为普遍。操作时是把五度收窄2音分、四度放宽2音分(对应于每秒约一个拍的拍频)，亦即把五度相生12次所产生的最大音差均布于各律之中，这样分出的12个半音基本上符合十二平均律的要求。

“纯点”的作用

传统的音乐理论通常把调式音阶中所构成的各种音程分为完全协和音程、协和音程、不完全协和音程及不协和音程四种。如下表。

表中所列的各种音程并未表明律制，是笼统而言。实际上，不同律制所生成的音的高度有许多是不一样的，因此所构成的同名音程的协和程度也是不一样的。十二平均律的同度、八度与纯律、五度相生律的是完全相同的；而其纯五度、纯四度、大三度、大六度、小三度、小六度的协和性却不同程度的低于纯律的同种音程.

人的耳朵更偏爱协和，愈是协和的音程愈能精确地：分辨。因此，在钢琴上调同度、八度是较容易的事；调“纯正”(指纯律)的四度、五度、三度、六度也不难；而要把它们调得符合十二平均律的要求就不那么轻而易举了。为了能使十二平均律在钢琴上得以应用，前人为我们找到了两个很有效的方法：一是利用纯正音程的“纯点”(无拍)；二是利用因非纯而形成的拍音。

调式音阶中所构成的四种音程

生活中我们都有这样的经验：当要说明某地或某建筑物在何处时，往往会借助于一个大家都较熟悉的地名或建筑。譬如：河北省廊坊市的地理位置是在北京市东南约70公里处，或说在天津市西北约60公里处。在钢琴基准音组的分律中，情形与此有些相似，只不过这里是把音程的“纯点”作为参照点，把音程的放宽与收窄作为方向、方位指示，把拍音的快慢作为尺度。譬如：调平均律四度音a→d1时，先把d1音调到纯正无拍，并顺势将其再调高一些，达到每秒一个拍音，这时的d1音，就是合于十二平均律要求的音高了。

有了纯正音程的“纯点”位置作为参照点，再辅以对定量拍频的听辨，把基准音组中的12个音分平均，无疑已不再是难以做到的事了。

吻合谐音

在讲拍的形成原因之前，有必要先交待一下“吻合谐音”★[z2] 这个概念。

前面已经讲到：一条弦的振动是一种很复杂的振动。它的横振动中包含许多相互间频率呈整数比的谐音。说到吻合谐音，自然是指二条弦或二条以上的弦之间所存在的频率相一致的谐音，不妨在此给它下一个较为严密的定义：

如果乐音fl的某次谐音与乐音f2的某次谐音的频率相等，称这两个谐音为乐音f1和乐音f2的吻合谐音。

从理论上讲，任何两个频率呈整数比的音之间，都存在吻合谐音，只不过频率比不同时吻合谐音的分布密度亦不同。而从调律的实用角度而言，我们所关心的只是那些频率呈简单整数比的四度、五度、三度、六度音程中的序数最低的那一组吻合谐音。

下图示出几种纯正音程的吻合谐音的次序关系(音名前的数字为谐音序号，下面的数字为频率)。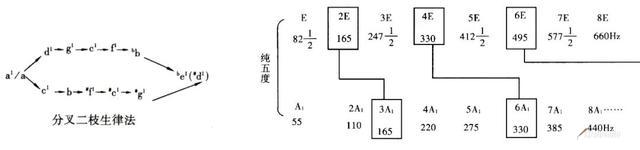

可看出纯正五度冠音的第二、第四、第六等谐音分别与根音的第三、第六、第九谐音为吻合谐音。

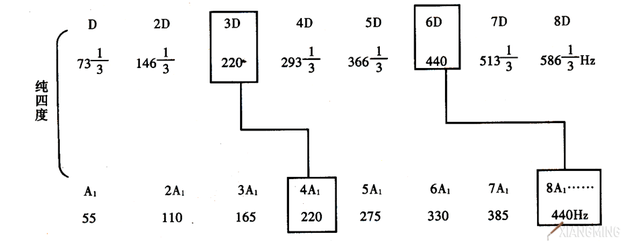
可看出纯正四度冠音的第三、第六等谐音，分别与根音的第四、第八等谐音为吻合谐音。

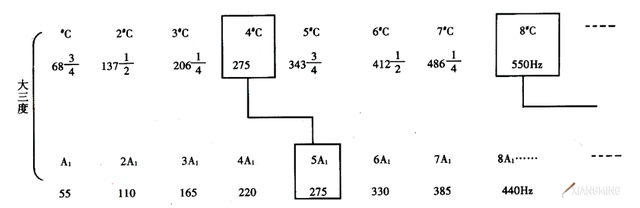
可看出纯正大三度冠音的第四、第八等谐音，分别与根音的第五、第十等谐音为吻合谐音。

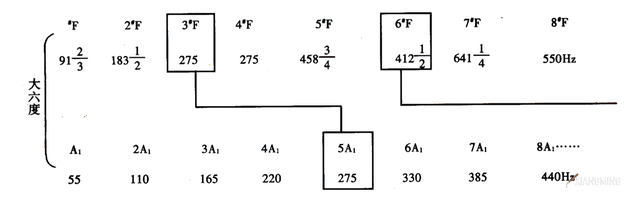
可看出纯正大六度冠音的第三、第六等谐音，分别与根音的第五、第十等谐音为吻合谐音。

综上，我们可以将钢琴调律中可能应用到的几种纯正音程的冠音与根音间的吻合谐音序数(仅取序数最低的一组)列出，再附以各种音程的频率比，能帮助我们认识到吻合谐音的序数关系及其与频率比之间的内在联系。牢记这种关系与联系，有利于以后学习和掌握拍频的计算。

八度 频率比2：1 吻合谐音冠一根二

纯五度 频率比3：2 吻合谐音冠二根三

纯四度 频率比4：3 吻合谐音冠三根四

大三度 频率比5：4 吻合谐音冠四根五

大六度 频率比5：3 吻合谐音冠三根五

小三度 频率比6：5 吻合谐音冠五根六

小六度 频率比8：5 吻合谐音冠五根八

拍音的形成与拍频的求法

1.拍音的形成

拍是因频率不同的两个声波的相互干涉而产生。两个频率不同的简谐量相加而形成的周期性幅值变化称为拍。

下图所示为一个6Hz与一个5Hz声波及它们叠加后的声波。由于这两个声波相差1Hz，叠加后每秒钟幅值起伏一次，即产生1拍／秒的拍频。

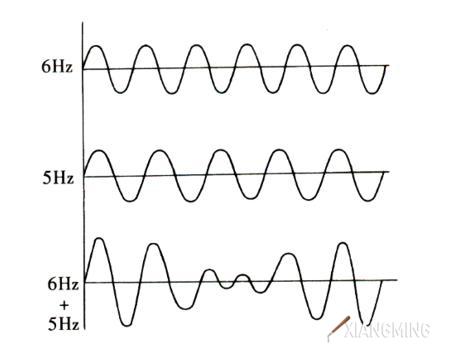
弦振动的各谐波成分可视为简谐量。幅值的变化是指波动强度的变化。如果构成某种纯正音程的根、冠两音的吻合谐音的频率出现偏离，其合成波就会出现周期性的幅值变化，从而也就会产生我们所能感受到的拍音。

十二平均律各种音程的频率比不像纯律音程那样呈简单的整数化，因此在纯律音程中原来存在的吻合谐音，在十二平均律的对应音程中却变得不吻合或不很吻合了。

如平均律纯五度：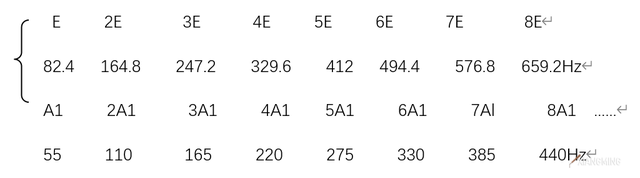

(因平均律纯五度的频率比值为1.498307，故E音基频为82.4Hz，与前面举纯律的例子不同)。

从这个例子可看出，由于律制不同，其冠音中各谐音的频率较之纯律均发生了变化，纯律中冠二根三的吻合谐音在这里变得不完全吻合了，2E(164.8Hz)与3A1(165Hz)之间出现了0.2Hz的偏差，因此必然产生每秒0.2次的拍音。

2.拍频的求法

计算十二平均律音程的拍频时，首先确认根、冠二音的基频，然后找到对应于纯正音程的频率比。算式可分为上行与下行音程两种。上行时为：冠音频率乘以频率比的后项，减去根音频率乘以频率比的前项；下行时反之。现举几个上行音程的拍频计算的例子：

例① 求平均律五度a—e1的拍频(先从乐音频率表查出或由a1求出a和e1的频率)。

已知：根音a的基频为220Hz，冠音e1的基频为329.63Hz，纯正五度的频率比为3：2。那么

(329.63×2)－(220×3)＝659.26－660＝－0.74(拍／秒)

答：平均律五度a→e1的拍频为0.74拍／秒，是负拍。

这里出现负数是因为调平均律上行五度时，需调得比“纯点”低一些(约2音分)。如果高于“纯点”，即为正拍。

例② 求平均律四度a，d1的拍频。

已知：根音a的基频为220Hz，冠音d1的基频为293.66Hz，纯正四度的频率比为4：3。那么

(293.66× 3)－(220×4)＝880.98－880＝0.98(拍／秒)

答：平均律四度a→d1的拍频为0.98拍／秒。

例③ 求平均律大三度a→#c1的拍频。

已知：根音a的基频为220Hz，冠音#c1基频为1277.18Hz，纯正大三度的频率比为5：4。那么

(277.18×4)－(220×5)=1108.72－1100＝8.72 (拍／秒)

答：平均律大三度a→#c1的拍频为8.72拍／秒。

例④ 求平均律大六度a→#f1的拍频。

已知：根音a的基频为220Hz，冠音#f1的基频为369.99Hz，纯正大六度的频率比为5：3。那么

(369.99×3)＝(220×5)=1109.97－1100＝9.97(拍／秒)

答：平均律大六度a→#f1的拍频为9.97拍／秒。

例⑤ 求平均律小三度a→c1的拍频。

已知：根音a的基频为220Hz，冠音c1基频为261.63Hz，纯正小三度的频率比为6：5。那么

(261.63×5)－(220×6)=1308.15－1320=－11.85(拍／秒)

答：平均律小三度a→c1的拍频11.85拍／秒，是负拍。

例⑥ 求平均律小六度a→f1的拍频。

已知：根音a的基频为220Hz，冠音f1的基频为349.23Hz，纯正小六度的频率比为8：5。那么

(349.23×5)－(220× 8)=1746.15－1760=－13.85(拍／秒)

答：平均律小六度a→f1的拍频为13.85拍／秒，是负拍。

下行音程拍频的计算是将根音放在前面。如求平均律下行五度e1→a的拍频：

(220× 3)－(329.63×2)=660－659.26=0.74(拍／秒)

这里，拍频的绝对值与前面例①完全一样，只是上行为负数，下行为正数。这是因为平均律五度窄于纯正五度，上行时需将冠音由“纯点”降低2音分，下行时需将根音由“纯点”升高2音分。冠音降低与根音升高，目的和结果是一样——收窄音程，使其符合平均律五度的要求。

有一个情况需要说明，在钢琴调律中，有时会同时出现速率不同的两种拍音，这主要发生在五度音程中。因为纯正五度的几组吻合谐音较密集，位次靠下，振幅相对较大，所以调平均律五度时，除冠二根三上的拍音之外，有时还能听到不太明显的冠四根六上的拍音。由于冠四根六上的拍音比冠二根三上的拍音快一倍，会干扰对拍频的听辨，这点要有心理准备。一旦遇上，悉心听辨，还是能够把它们区分开的。

拍频的规律

1.同音程不同音高的拍频

同一种音程的拍频，随乐音频率的变化而变化。音程向高音区平移时拍频趋快，音程向低音区平移时拍频趋慢。拍频的变化与乐音(根音或冠音)频率的变化成正比。

试举一例如以说明(为精确起见，根音、冠音的频率及音程的拍频均取六位小数)：

十二平均律纯四度音程e1→a1的拍频为：

(440×3)－(329.627557×4)=1320－1318.510228=1.489772(拍／秒)

将e1→a1这个四度音程向高音区平行推移至a1→d2时，则a1→d2的拍频为：

(587.329536× 3)－(440×4)=1761.988608－1760=1.988608(拍／秒)

再将e1→a1这个四度音程向低音区平行推移至b→e1时，则b→e1的拍频为：

(329.627557× 3)－(246.941651 ×4)=988.882671－987.766604=1.116067(拍／秒)

计算表明： 音程向高音区平移时拍频趋快(1.988608>1.489772)；音程向低音区平移时拍频趋慢(1.116067<1.489772)。

现在来看看音程平移后，乐音频率的变化与音程拍频的变化之间的关系。由上计算可知，e1→a1与a1→d2这两个相距纯四度的纯四度音程的拍频比值为：

1.988608／1.489772=1.334840

这个比值恰等于平均律纯四度的频率比值()5／1=1.334840。可见，对于同一种音程来说，当它向高(或低)音区平移时，其拍频的变化与其根音(或冠音)频率的变化是成正比的。

既然拍频的变化与构成音程的乐音的频率变化成正比，那么我们在求音程的拍频时就可加以利用。如我们已知f→c1这个五度的拍频为0.59拍／秒，求#f→#c1五度的拍频时，只要将0.59(拍／秒)乘上平均律半音的频率比值(1.059463)就可以了。如下：

0.59X1.059463=0.63(拍／秒)

求e→b五度的拍频时，则除1.059463，即：

0.59÷1.059463=0.56(拍／秒)

这样，计算起来就简单多了。

2.同根音的不同音程的拍频

在同一音(做根音)上建立起来的不同音程，拍频是按五度、四度、大三度、大六度、小三度、小六度之顺序逐个加快。其中：五度、四度的拍频相对较慢；大三、大六度的拍频加快了许多；小三、小六度的拍频更快。

上面所举的6个拍频计算的例子很好地说明了这一点。为了使这种关系体现得更直观、更明确，现将这六种音程的算式与拍频简列于下：

五度(e1)329.63×2－(a)220× 3=0.74(拍／秒)

四度(d1)293.66×3－(a)220×4=0.98(拍／秒)

大三(#c1)277.18×4－(a)220×5=8.72(拍／秒)

大六(#f1)369.99× 3－(a)220×5=9.97(拍／秒)

小三(c1)261.63×5－(a)220×6=－11.85(拍／秒)

小六(f1)349.23×5－(a)220× 8=－13.85(拍／秒)

如此的不同音程拍频的快慢顺序，每一位钢琴调律者都应该做到心里有数。因为它在基准音组生律与校验中非常有用。但对于其中具体的拍数不能死记，只能活用，因为一种音程一旦移位，它的拍频就会发生变化。

3.正拍和负拍

钢琴调律中，有些音程需要放宽，有些音程需要收窄。原因很简单，十二平均律的音程不同于纯律音程，有的宽出一些，有的窄进一些(参见第四章第六节“三律”主要音程比较表)。

具体来说，平均律四度、大三度、大六度音程宽于纯正音程，而五度、小三度、小六度音程窄于纯正音程。因此，调四度或大三、大六度时是在纯正音程基础上放宽，而调五度或小三、小六度时是在纯正音程基础上收窄。

需要注意的是，放宽或收窄在上行与下行调律中的操作方法是不一样的。现以四度、五度为例加以说明：

五度收窄，上行时是将冠音由“纯点”降低2音分，下行时将根音升高2音分；

四度放宽，上行时是将冠音由“纯点”升高2音分，下行时将根音降低2音分；

这就像把一个立柱加长或去短那样，倘若把它去短，可以截上头，也可以截下头，结果是一样的。只是截上头时顶端降低，截下头时底端升高。

音程的收窄或放宽，都是针对纯正音程的“纯点”而言的。调五度、小三度、小六度，上行是把冠音由“纯点”降低一些，这时产生的拍称为负拍；下行则是把根音由“纯点”升高一些，这时产生的拍称为正拍。调四度、大三度、大六度，上行是把冠音由“纯点”升高一些，这时产生的拍称为正拍；下行则是把根音由“纯点”降低一些，这时产生的拍称为负拍。简单地说：高于“纯点”时所产生的拍为正拍；低于“纯点”时所产生的拍为负拍。

放宽与收窄、正拍与负拍是两种既紧密联系，又有本质区别的概念。宽与正、窄与负，切不可简单地等同。

4.转位音程的拍

一种音程可以向上转位，也可以向下转位。向上转位时，转位音程的冠音通常比原位音程的根音高一个八度(这里不考虑复音程转位)；向下转位时，转位音程的根音通常比原位音程的冠音低一个八度。也就是说，原位音程加上转位音程为八度音程(如下图)。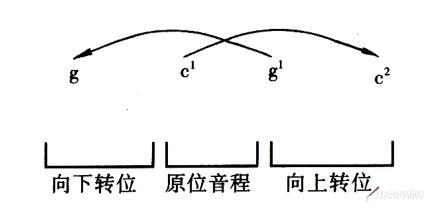

作为钢琴调律工作者，要关心四五度和三六度的转位，因为调律中常常会用到它们。下面写出它们的转位关系。

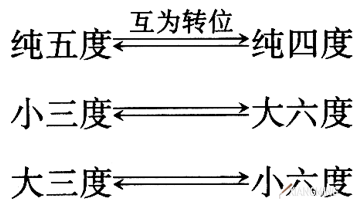
由于转位音程的根音(或冠音)与原位音程的冠音(或根音)通常构成八度音程，频率比是2：1或1：2，而且两个音程有一个共用的音，因此转位音程与原位音程间存在着一种拍频互补关系。亦即它们的拍频绝对值或是相等，或是其一为另一的2倍。

四度、五度转位的拍频互补关系：四度在高位、五度在低位时，四度的拍频是五度的2倍；反之，四度在低位、五度在高位时，四度与五度的拍频相等。下式：

大三度、小六度转位的拍频互补关系：小六度在高位、大三度在低位时，小六度的拍频是大三度的2倍；反之，小六度在低位、大三度在高位时，小六度与大三度的拍频相等。见下式：

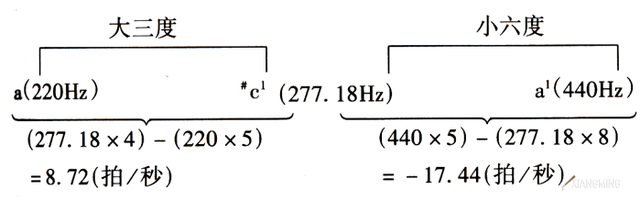
(小六度在高位，其拍频绝对值是大三度拍频的2倍。)

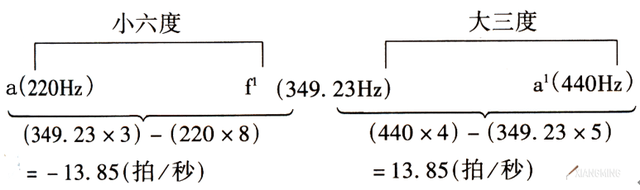
(小六度在低位，其拍频绝对值与大三度的拍频相等。)

小三度、大六度转位的拍频互补关系：小三度在高位、大六度在低位时，小三度的拍频是大六度的2倍；反之，小三度在低位、大六度在高位时，小三度与大六度的拍频相等。见下式：

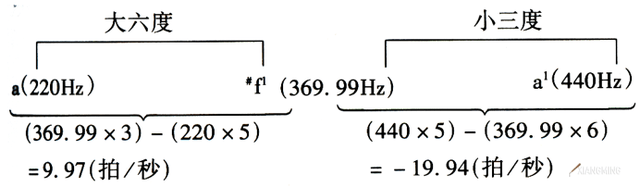
(小三度在高位，其拍频绝对值是大六度拍频的2倍。)

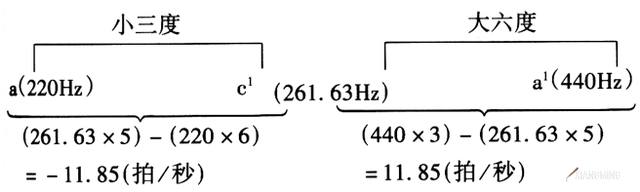
(小三度在低位，其拍频绝对值与大六度拍频相等。)

至此，将上述三种转位音程的拍频互补关系做这样的归纳，以便于记忆：

对于四度五度、小三大六、大三小六几种转位音程来说，如果四度、小三度、小六度在高位，它们的拍频分别是五度、大六度、大三度拍频的2倍；反之，则四度与五度、小三与大六、小六与大三的拍频相等(此处不考虑正拍与负拍)。

基准音组的音区定位

基准音组所处的音区，各国、各地区、各人的定位虽不尽一致，但大体不会超出d—c2这个范围，且更多的人是选在f→e1位置。这是因为人们在遵循着一个共同的原则：其间

四度、五度拍频表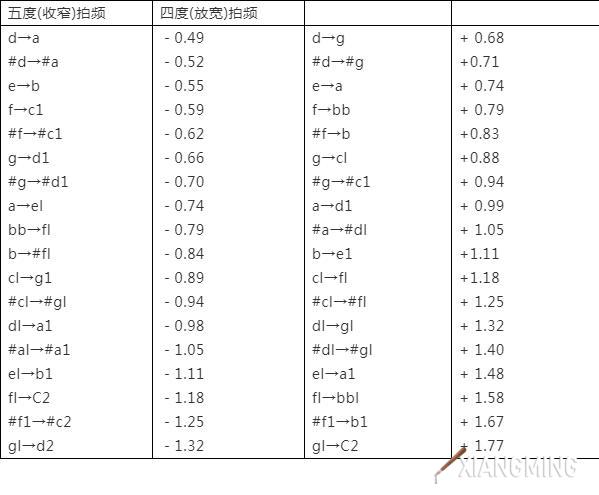

四度、五度的拍频接近1拍／秒，人耳较易听辨。另外，在此音区内，三度、六度的拍频不至于过快；而且音区的下限音最好不要涉及到泛音较强、非谐成分相对明显的缠弦。

看看下面的四度、五度拍频表(上表)★[z3] 就不难理解人们为什么通常要将基准音组设定在d—c2音区之内了。

此间，五度音程的拍频最低为0.49拍／秒，最高为1.18拍／秒；四度音程的拍频最低为0.68拍／秒，最高为1.77拍／秒。两种音程的拍频均在1拍／秒上下。有人出于更精微的考虑，建议将基准音组定位在四度、五度拍频不超出±一又三分之一拍／秒的音区之内。亦有人认为，实际的调律毕竟不能机械地依赖于计算的结果，考虑到钢琴的声学结构、调律的稳定性及A－440音叉的普遍应用等，把基准音组定位在a－#g1，更宜。

钢琴调律是一个传统意识较强的专业，一旦掌握了这门技术，要中途改变已熟悉的操作方法与程序是件不容易的事情，似乎也没有这种必要。年轻一些的调律者，思想更活跃，实践中不妨试探、比较一下基准音组定位的多种可能性，看看哪种定位更合理、更实用。

音准曲线的成因

测试结果表明：一台由调律师调准了的钢琴，它的88个音的高度并非完全符合理论计算的结果，而是只在中音区(c－c2)大体接近理论值，由c2向上渐趋偏高，由c向下则渐趋偏低，最高音、最低音的最大偏差可达30音分上下。

下图显示一位专业调律师所调琴的实测结果(锯齿状连线)，以及取实测坐标点平均值而勾勒出的圆滑的音准曲线。由图不难看出：①钢琴的调律，低音偏低、高音偏高是一种客观存在，而非人有意使然；②人耳听觉误差所造成的音高偏离，伴随着钢琴全音域内的音。

那么，音准曲线是如何形成的呢?主要原因有两个：一是人的生理、心理因素，二是琴弦的固有物理属性。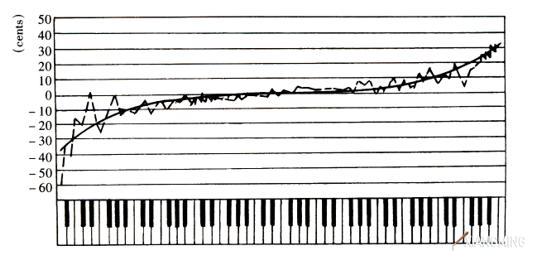

1.人的生理心理因素

入耳对于不同频率的听觉锐度(感受灵敏度)不一样。前面讲到，人耳对1000Hz附近的振动最敏感，随着频率的不断升高或降低，听觉锐度会下降。这是生理上所决定的。另外，人的心理八度要比数理八度宽一点，要求更高或更低一些的夸张才觉得准了，而这种夸张要求的具体量值是因人而异的。

2.琴弦泛音的非谐性

前面已讲到，一条理想弦的频率可用下式表达：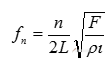

公式表明，理想弦的各次泛音的频率为基频的整数倍。而实际应用的钢琴弦并非理想弦，它的柔顺度不足，受劲度以及均匀度等影响，其泛音频率与基频之间呈现较为复杂的关系，存在“非谐性”，即略偏高于基频的整数倍。这样，在八度扩展调律中，由于冠音的音高是由根音的二次谐波(第一泛音)来确定，必然形成向高音区逐渐偏高、向低音区逐渐偏低的音准曲线。

为使弦振动泛音的频率计算更切合实际，须给上述公式加一个修正项。即：

可写成：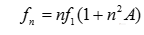

式中的“n2A"是针对不同谐波频率的修正项。“A”为由琴弦长度、直径、张力及纵向弹性模量等共同决定的量。由此可见，规格型号不同的钢琴，修正量不一样，谐音的非谐程度不一样。从而导致音准曲线上的差异。

上述公式修正项中的“A”，在取值上都是经验性的。

这里仅举一例★[z4] ：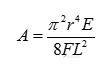

以上式中:

fn —— n次谐音的频率；

f1 —— 第一谐音(即基音)的频率；

E —— 弹性模量；

r —— 弦半径；

L —— 弦长度；

F —— 张弦力。

从经验公式可看出：琴弦长、张力大时，泛音的非谐程度低，频率的偏移量相对小些；琴弦粗时，泛音的非谐程度高，频率的偏移量相对大些。

讲到这里，不但大致清楚了钢琴音准曲线的形成原因，而且还会发现钢琴的音准曲线并非是惟一的，不同规格的钢琴甚至不同人调出的同一台钢琴会表现出不同的曲线特征(亦即高音偏高、低音偏低的程度会有差异)。当然，总的趋向应该是一致的。取其平均值，可以用以体现一般性状况。

十二平均律音级与频率实用换算方法

如果你有一本《十二平均律音级与频率对照表》，就可以从中查到由大字一组C至小字五组c音之间的所有音级(律音及音分)所对应的频率值；也可反过来用之，即查找某一频率所对应的音级及其增减的音分数。但是超出C1一c5这个范围的音级通常就查不到了。

下面列出的两个实用算式★[z5] ，就可弥补上述“对照表”之不足，而且用起来很方便。

式一：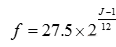

式中：f为频率；J为钢琴键的序号，对应各八度组的不同音名(如第1键为大字二组的A音，第49键为小字一组A音)。J可以是小数，小数点后第一位为音分的十分数，小数点后第二位为音分的个位数。这样，你就可以用算式求出钢琴上任何一个琴键(音)乃至偏离若干音分时的频率值。

例①：求c2音的频率。

已知c2是第52键.代入式：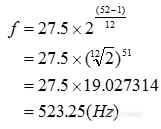

答案：c2音的频率为523.25Hz。

例②：求a1＋15音分时的频率。

已知a1是第49键，代人式：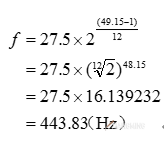

答案：a1＋15音分时的频率为443.83Hz。

用这个算式还可以求出高于c5的音的频率。高于c5的音可由88向上顺序编号，如＃c5为89，d5为90，＃d5为91等等。

例③：求比钢琴最高音c5还高大二度的d5的频率。

已知d5对应于第90键，代人式：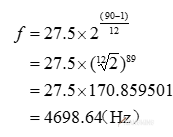

答案：d5音的频率为4698.64Hz。

式二：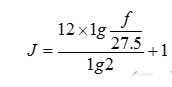

利用这个算式可以求出高于27.5Hz(含27.5Hz)的任何频率所对应的键号(音级)。计算结果如出现小数，小数部分为音分数。

例④ 求2000Hz所对应的音级。

已知f为2000Hz，代人式：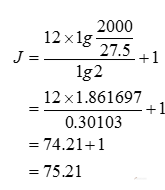

答案：2000Hz的音所对应的音级是b3＋21音分(第75键)。

例⑤：求4500Hz所对应的音级。

已知f为4500Hz，代人式：

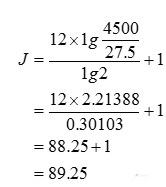
答案：4500Hz的音所对应的音级是＃c5＋25音分(相当于第89键)。

这两个算式，因设定的最低音是A2(27.5Hz)，因此不适于用来计算低于A：的音级。如果勉强利用，就需要把低于A2的键号设定为0，－1，－2等；涉及到小数(音分数)时，还须做一些变通。使用这两个算式，需配备一个函数计算器。

[z1]许音.钢琴调律方法论初步.乐器，1994年，(1).(2)期

z2w.B.怀特.钢琴调律与有关技术.王可茂译.北京：人民音乐出版社.1992.

[z3]①刘金寿.钢琴音准与基准音组位置的最佳选择.乐器.1997.1

[z4]引自ThomasD.Rossing：The ScienceSound.

[z5]算式引自《乐器》杂志1984年第4期高和“十二平均律音级(律音、音分)与频率的换算关系”一文。